Info Math SMA

Contoh soal tentang aplikasi materi turunan pada matematika SMA kali ini yaitu tentang aplikasi pada biaya produksi barang, aplikasi turunan fungsi pada biaya proyek dan aplikasi turunan pada volume bangun ruang.
Selamat menyimak dan tolong di share.

 SOAL 1 Aplikasi Turunan pada Biaya Produksi Barang
Diketahui biaya produksi barang sebuah perusahaan dinyatakan dalam fungsi f(x) = 8x² – 120x. Kemudian harga jual tiap barang dinyatakan dalam f(x) = 1/3 x² – 10x + 200. x menyatakan jumlah barang. Maka, untuk mencapai keuntungan maksimum, jumlah barang yang harus diproduksi adalah sebanyak…

PEMBAHASAN
Biaya Produksi = 8x² – 120x
Harga Jual tiap barang = 1/3 x² – 10x + 200
Keuntungan = Harga Jual semua Barang  – Biaya Produksi
= (Jumlah Barang dikali Harga Jual tiap Barang) – Biaya Produksi
= x.(1/3 x² – 10x + 200) – (8x² – 120x)
= (1/3 x³ – 10x² + 200x) – (8x² – 120x)
= 1/3 x³ – 18x² + 320x
Untuk mencapai keuntungan maksimum, maka nilai stationernya = 0
f ‘ (x) = 0
x² -36x + 320 = 0

(x -16)(x – 20) = 0
x = 16 atau x = 20.
Jadi, jumlah barang yang harus dijual adalah 16 atau 20 buah.

SOAL 2 Aplikasi Turunan pada Biaya Proyek
Biaya proyek sebuah perusahaan per harinya dinyatakan oleh fungsi f(x) = 3x + 1200/x – 60 (dalam juta rupiah). Tentukan total biaya produksi selama x hari agar diperoleh biaya minimum?

PEMBAHASAN
Biaya Proyek per hari = 3x + 1200/x – 60
Biaya Proyek per x hari = (3x + 1200/x – 60)/x
= 3 + 1200/x² – 60/x

= 3x² – 60x + 1200

Agar biaya minimum, maka nilai stationer = 0 atau f ‘ (x) = 0.
f ‘ (x) = 0
6x – 60 = 0
6x = 60
x = 10 hari.
Biaya minimum per hari
= 3x + 1200/x – 60
= 3(10) + 1200/10 -60
= 30 + 120 – 60
= 90 juta rupiah
Maka total biaya minimum proyek selama 10 hari adalah
= 90 juta rupiah x 10 hari
= 900 juta rupiah.

SOAL 3. Aplikasi Turunan pada Volume Bangun Ruang. 
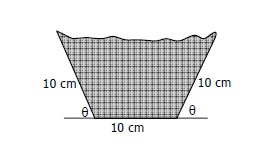
Sebuah talang air akan dibuat dari lembaran seng yang lebarnya 30 cm dengan melipat lebarnya atas menjadi 3 bagian yang sama, seperti terlihat pada gambar. Jika θ menyatakan besar sudut dinding talang dengan bidang alasnya, maka volume air yang tertampung paling banyak bila θ …

PEMBAHASAN
Lipatan seng berbentuk trapesium.
Untuk mencapai volume air maksimum, maka nilai stationer dari luas trapesium = 0.
Pembahasannya ada pada gambar di bawah ini.

Jadi untuk mencapai volume maksimum, besar sudut θ = 60°.

Semoga Manfaat

#Ikhitar itu WAJIB
UNIQUE TRADISIONAL @ INDONESIA, U KNOW ?? KLIK HERE PLEASE