Info Math for Education

Polinomial (suku banyak) dan Metode Horner

Posted byNyach

Pembagian Metode Horner

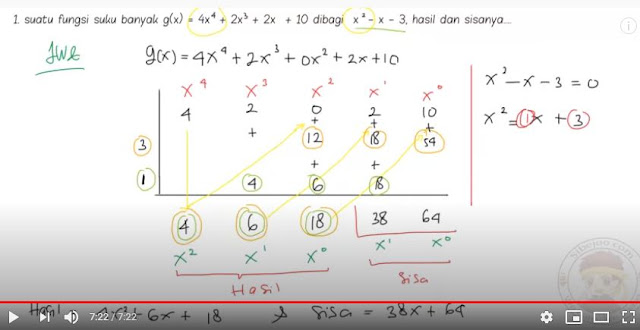
Cara Horner merupakan metode cepat untuk membagi suku banyak, tetapi cara ini hanya dapat digunakan jika pembaginya berbentuk x – k [ingat bahwa x + k = x – (–k)]. Dengan cara ini, kita hanya menuliskan bagian-bagian penting dalam pembagian bersusun. Mari kita bandingkan pembagian bersusun dengan cara Horner untuk membagi 6x³ + 43x² + 5x – 13 dengan x + 7.

Perhatikan bahwa dalam cara Horner kita singkat 6x³ + 43x² + 5x – 13 dengan hanya menuliskan koefisien-koefisiennya: 6, 43, 5, dan –13, dan kita tuliskan pembagi x + 7 dengan –7. (Dengan menuliskan –7 kita tidak perlu untuk melakukan pengurangan, melainkan penjumlahan. Tetapi penggantian tanda ini menyebabkan pergantian tanda juga pada bilangan-bilangan pada kotak warna abu-abu.)

Secara garis besar, cara Horner untuk membagi suku banyak berderajat tiga adalah sebagai berikut. (Cara Horner untuk suku banyak yang berderajat lebih tinggi memiliki pola yang serupa.)

Metode Horner (untuk Suku Banyak Berderajat Tiga)

Untuk membagi ax³ + bx² + cx + d dengan x – k, kita lakukan cara berikut.

Pola vertikal: Jumlahkan suku dalam kolom.
Pola horizontal: Kalikan hasilnya dengan k.

Contoh berikutnya menunjukkan bagaimana menggunakan cara Horner dalam pembagian suku banyak.

Contoh 3: Menggunakan Cara Horner

Gunakan cara Horner untuk membagi x⁴ – 5x³ – 2x² + 11x – 1 dengan x – 5.

Pembahasan Pertama kita tuliskan koefisien-koefisien yang bersesuaian untuk menunjukkan suku banyak yang dibagi dan pembagi.

Berdasarkan baris terakhir di atas, kita dapat melihat bahwa hasil baginya adalah x³ – 2x + 1 dan sisanya adalah 4. Sehingga

Polinomial (suku banyak) dan Metode Horner

Posted byNyach

Pada pembahasan ini kita akan mempelajari suku banyak secara aljabar. Sebagian besar diskusi kita nanti akan membahas tentang pemfaktoran suku banyak. Untuk memfaktorkan suku banyak, kita harus tahu bagaimana cara membagi suku banyak. Oleh karena itu, setelah mempelajari pembahasan ini diharapkan kita mampu

§ Menggunakan pembagian bersusun untuk membagi suku banyak dengan suku banyak lainnya.

§ Menggunakan cara Horner untuk membagi suku banyak dengan suku banyak lainnya yang berbentuk (x – k).

§ Menggunakan Teorema Sisa dan Teorema Faktor.

Pembagian Bersusun Suku Banyak

Pembagian suku banyak hampir sama dengan pembagian bilangan. Ketika kita membagi 46 dengan 5, hasil baginya adalah 9 dan sisanya adalah 1.

Untuk membagi suku banyak, kita gunakan pembagian bersusun yang dijelaskan sebagai berikut.

Algoritma Pembagian

Jika f(x) dan p(x) adalah suku banyak, dengan p(x) ≠ 0, maka ada suku banyak tunggal H(x) dan S(x), di mana S(x) adalah 0 atau suku banyak yang memiliki derajat kurang dari derajat p(x), sedemikian sehingga

atau,

Suku banyak p(x) disebut sebagai pembagi, H(x) merupakan hasil bagi, dan S(x) merupakan sisa.

Contoh 1: Pembagian Bersusun Suku Banyak

Bagilah 4x² – 14x + 15 dengan x – 4. Nyatakan hasilnya ke dalam masing-masing bentuk yang ditunjukkan pada Algoritma Pembagian.

Pembahasan Suku banyak yang akan dibagi adalah 4x² – 14x + 15, dan pembaginya x – 4. Pertama kita susun kedua suku banyak tersebut sebagai berikut.

Selanjutnya kita bagi suku pertama terbagi dengan suku pertama pembagi untuk mendapatkan suku pertama hasil bagi: 4x²/x = 4x. Kemudian kita kalikan pembagi dengan 4x dan kita kurangkan terbagi dengan hasil yang diperoleh.

Kita ulang proses ini dengan menggunakan baris terakhir 2x + 15 sebagai yang terbagi.

Proses pembagian berakhir ketika baris terakhir memiliki derajat yang kurang dari derajat pembagi. Baris terakhir merupakan sisa, sedangkan baris yang paling atas merupakan hasil bagi. Pembagian di atas dapat dinyatakan dalam dua bentuk berikut.

Contoh 2: Pembagian Bersusun Suku Banyak

Misalkan f(x) = 12x⁴ – 10x³ + 8x – 3 dan p(x) = 2x² – x + 4. Tentukan suku banyak H(x) dan S(x) di mana f(x) = p(x) ∙ H(x) + S(x).

Pembahasan Sebelum melakukan pembagian bersusun, kita sisipi suku 0x² pada suku banyak yang akan dibagi agar suku banyak tersebut memiliki suku yang lengkap.

Proses pembagian tersebut sudah selesai karena 3x + 49 memiliki derajat yang lebih rendah daripada 2x² – x + 4. Berdasarkan pembagian bersusun di atas kita dapat melihat bahwa H(x) = 6x² – 2x – 13 dan S(x) = 3x + 49, sehingga

Pembagian suku banyak yang tidak linier

Posted byNyach

Pembagian suku banyak atau polinomial dengan pembagi tidak linier.
Tidak linier atau berpangkat lebih dari satu sebagai pembagi dari suku banyak

Perlu diperhatikan !!!
Jika:
suku banyak P(x) berderajat n
Pembagi dari berderajat m
Maka :
>>Hasil Baginya mempunyai variabel berpangkat (n-m)

>>Sisa pembagian mempunyai variabel berpangkat (m-1)

(2x⁴ – 5x³+8x² – 6x+4):(x² – x +2)
n = 4
m = 2
Hasil bagi berpangkat (4-2) yaitu 2
Sisa pembagian berpangkat (2-1) yaitu 1

cara Pembagian suku banyak atau polinomial dengan pembagi tidak linier kita bisa menggunakan cara pembagian tersusun (bhs jawa : poro gapit) juga bisa menggunakan metode Horner.

Iya menggunakan metode Horner bukankah selama ini Anda menggunakan metode horner untuk pembagian yang di bagi dengan variabel pangkat satu.

Metode Horner yang digunakan untuk pembagi yang tidak linier di temukan oleh orang Indonesia yang bernama SUKINO dan beliau memberi nama HORNER KINO.

BAGAN HORNER KINO DERAJAT DUA Sebagai berikut :

Soal dan Pembahasa Aplikasi Turunan Fungsi

Posted byNyach

Contoh soal tentang aplikasi materi turunan pada matematika SMA kali ini yaitu tentang aplikasi pada biaya produksi barang, aplikasi turunan fungsi pada biaya proyek dan aplikasi turunan pada volume bangun ruang.
Selamat menyimak dan tolong di share.

SOAL 1 Aplikasi Turunan pada Biaya Produksi Barang
Diketahui biaya produksi barang sebuah perusahaan dinyatakan dalam fungsi f(x) = 8x² – 120x. Kemudian harga jual tiap barang dinyatakan dalam f(x) = 1/3 x² – 10x + 200. x menyatakan jumlah barang. Maka, untuk mencapai keuntungan maksimum, jumlah barang yang harus diproduksi adalah sebanyak…

PEMBAHASAN
Biaya Produksi = 8x² – 120x
Harga Jual tiap barang = 1/3 x² – 10x + 200
Keuntungan = Harga Jual semua Barang – Biaya Produksi
= (Jumlah Barang dikali Harga Jual tiap Barang) – Biaya Produksi
= x.(1/3 x² – 10x + 200) – (8x² – 120x)
= (1/3 x³ – 10x² + 200x) – (8x² – 120x)
= 1/3 x³ – 18x² + 320x
Untuk mencapai keuntungan maksimum, maka nilai stationernya = 0
f ‘ (x) = 0
x² -36x + 320 = 0

(x -16)(x – 20) = 0
x = 16 atau x = 20.
Jadi, jumlah barang yang harus dijual adalah 16 atau 20 buah.

SOAL 2 Aplikasi Turunan pada Biaya Proyek
Biaya proyek sebuah perusahaan per harinya dinyatakan oleh fungsi f(x) = 3x + 1200/x – 60 (dalam juta rupiah). Tentukan total biaya produksi selama x hari agar diperoleh biaya minimum?

PEMBAHASAN
Biaya Proyek per hari = 3x + 1200/x – 60
Biaya Proyek per x hari = (3x + 1200/x – 60)/x
= 3 + 1200/x² – 60/x

= 3x² – 60x + 1200

Agar biaya minimum, maka nilai stationer = 0 atau f ‘ (x) = 0.
f ‘ (x) = 0
6x – 60 = 0
6x = 60
x = 10 hari.
Biaya minimum per hari
= 3x + 1200/x – 60
= 3(10) + 1200/10 -60
= 30 + 120 – 60
= 90 juta rupiah
Maka total biaya minimum proyek selama 10 hari adalah
= 90 juta rupiah x 10 hari
= 900 juta rupiah.

SOAL 3. Aplikasi Turunan pada Volume Bangun Ruang.
Sebuah talang air akan dibuat dari lembaran seng yang lebarnya 30 cm dengan melipat lebarnya atas menjadi 3 bagian yang sama, seperti terlihat pada gambar. Jika θ menyatakan besar sudut dinding talang dengan bidang alasnya, maka volume air yang tertampung paling banyak bila θ …

PEMBAHASAN
Lipatan seng berbentuk trapesium.
Untuk mencapai volume air maksimum, maka nilai stationer dari luas trapesium = 0.
Pembahasannya ada pada gambar di bawah ini.

Jadi untuk mencapai volume maksimum, besar sudut θ = 60°.

Semoga Manfaat

#Ikhitar itu WAJIB

Soal Turunan Fungsi Aljabar dan Pembahasannya (Latihan siswa kelas XI program IPS) KTSP

Posted byNyach

Agar bisa matematika itu banyak caranya, salah satunya dengan mengamati hasil pekerjaaan (pembahasan soal) dari orang lain sampai mengerti.

CARA JITU BELAJAR MATEMATIKA DARI ORANG LAIN
1. Amati hasil pembahasan soal dengan baik. Setelah kita yakin bahwa kita mengerti tentang pembahasan itu silahkan ditutup pembahasannya tapi soalnya silahkan Anda di salin.
2. Kemudian kerjakan soal tersebut tanpa melihat pembahasan sampai selesai. Jika lupa usahakan mengingat-ingat jangan buru-buru membuka pembahasan.
3. Apabila benar2 tidak ingat, silahkan tutup pekerjaan Anda, dan ganti membuka pembahasan. Silahkan membaca pembahasan dari awal sampai akhir sehingga yakin benar-benar paham. ULANGI LANGKAH 1 .
SEMOGA SUKSES

SOAL TURUNAN FUNGSI ALJABAR DAN PEMBAHASANNYA.
Soal No. 1
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 3x⁴ + 2x² − 5x
b) f(x) = 2x³ + 7x

Soal Fungsi komposisi (kelas XI IPS) KTSP

Posted byNyach

Suatu fungsi akan memetakan setiap anggota domain dengan tepat satu anggota kodomain. Jika anggota kodomain tersebut dipetakan lagi oleh fungsi lain ke kodomain berikutnya, maka akan diperoleh pemetaan yang berkesinambungan. Pemetaan yang berkesinambungan seperti itu disebut komposisi fungsi.

Berikut ini adalah soal-soal fungsi komposisi silahkan digunakan dikerjakan dan hasilnya di tunjukan ke guru atau fasilitator Anda.

SOAL :

Nomor 1
Jika f(x) = x – 5 dan g(x) = x² – 1 maka (f o g)(x) = …
A. x² – 6
B. x² – 10x – 24
C. x² – 10x + 26
D. x² – 4
E. x² – 10x + 24

Nomor 2
Jika f(x) = x – 1 dan g(x) = x² – 7 maka (g o f)(3) = …
A. 3
B. 2
C. 1
D. – 2
E. – 3

Nomor 3
Misal
f(x) = 3x² – 1

Nilai dari (f o g) (3) = …
A. 2
B. 3
C. 4
D. 65
E. 74

Nomor 4
Jika (f o g) (x) = 6x – 3 dan f(x) = 2x + 5 maka g(x) = …
A. 4x – 8
B. 3x – 4
C. 3x + 4
D. 2x – 4
E. 2x + 4

Nomor 5
Jika (f o g)(x) = x² – 4 dan g(x) = x + 3, maka f(x) = …
A. x² – 6x + 13
B. x² – 6x + 5
C. x² + 6x + 5
D. x² – 1
E. x² – 7

Soal Uraian :
Nomor 1
Data:
f(x) = 3x + 2
g(x) = 2 − x
Tentukan !
a) (f o g)(x)
b) (g o f)(x)

Nomor 2
Diberikan dua buah fungsi:
f(x) = 3x² + 4x + 1
g(x) = 6x

Tentukan:
a) (f o g)(x)
b) (f o g)(2)

Selamat mengerjakan soal komposisi fungsi, materi mata pelajaran matematika kelas XI IPS sesuai kurikulum KTSP 2006.

Menentukan peluang Kejadian Binomial

Posted byNyach

Menentukan peluang Kejadian Binomial - Distribusi Binomial adalah salah satu materi kelas XI pada kurikulum 2013.Dalam teori probabilitas dan statistika, Distribusi Binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak yang saling bebas, dimana setiap hasil percobaan memiliki
probabilitas p.Pengertian tersebut menurut wikipedia.org

Ciri-ciri percobaan binomial yaitu sebagai berikut.

Setiap percobaan dibedakan menjadi 2 jenis kejadian yang keduanya saling lepas
Hasil dari percobaan tersebut hanya 2 macam, yaitu berhasil dan gagal
Peluang kejadian berhasil adalah p dan peluang kejadian gagal adalah q = 1-p
Masing-masing percobaan bersifat saling bebas, artinya hasil percobaan pertama tidak memengaruhi hasil percobaan berikutnya.

Jika percobaan binomial dilakukan berulang-ulang sampai n kali, peluang diperoleh sukses sebanyak x dapat dihitung dengan rumus berikut.

$\LARGE P\left ( X = x \right ) = b\left ( x; n; p \right ) = _{n}C_{x} \times p^{x} \times q^{n-x}$

dengan x = 0, 1, 2, 3, ..., n
Keterangan :
n : banyak percobaan
x : banyak berhasil
p : peluang berhasil
q : peluang gagal (q = 1-p)

Contoh Soal Dan Pembahasan

Sebuah mata uang logam dilemparkan sebanyak 8 kali.Berapa peluang muncul gambar sebanyak 5 kali?

Diketahui :
n = 8
x = 5
p = 1/2
q = 1-p = 1- 1/2 = 1/2
Ditanya : peluang muncul gambar sebanyak 5 kali
Jawab :
$P(X = 5) = b(5; 8; \frac{1}{2})$
$= _{8}C_{5} \times p^{5} \times q^{8-5}$
$= \frac{8!}{5! \times 3!} \times (\frac{1}{2})^{5} \times (\frac{1}{2})^{3}$

$= \frac{8 \times 7 \times 6}{3 \times 2 \times 1} \times \frac{1}{32} \times \frac{1}{8}$

$= 56 \times \frac{1}{32} \times \frac{1}{8} = \frac{7}{32}$

Jadi, peluang muncul gambar sebanyak 5 kali adalah 7/32

Sebuah dadu dilemparkan sebanyak 5 kali.Berapa peluang muncul mata dadu 4 sebanyak 2 kali?

Diketahui :
n = 5
x = 2
p = 1/6
q = 1-1/6 = 5/6
Ditanya : peluang muncul mata dadu 4 sebanyak 2 kali
Jawab :
$P(X = 2) = b(2; 5; \frac{1}{6})$
$= _{5}C_{2} \times p^{2} \times q^{5-2}$
$= \frac{5!}{2! \times 3!} \times (\frac{1}{6})^{2} \times (\frac{5}{6})^{3}$

$= \frac{5 \times 4}{2\times 1} \times \frac{1}{36} \times \frac{125}{216} = \frac{625}{3888}$

Jadi, peluang muncul mata dadu 4 sebanyak 2 kali adalah 625/3888

Panjang Latus Rectum Pada Elips

Posted byNyach

Tentang panjang latus rectum pada Elips ini materi yang terasa kurang viral (terkenal) atau boming. Latus Rectum paling terkenal saat pembahasan Irisan kerucut tentang Parabola. Definisi Latus Rectum pada elips adalah tali busur yang melalui salah satu fokus dan tegak lurus dengan sumbu mayor.

Sedangkan titik potong latus rektum dengan ellips disebut latera rekta. Untuk mencari panjang latus rektum diberikan nilai $x=c=\sqrt{a^{2}-b^{2}}$ pada persamaan (4) dan dengan menyelesaikan persamaan untuk y diperoleh y = b²/a. Jadi latera rekta ellips (4) adalah L(c, b²/a) dan R(c, –b²/a), sehingga panjang latus rektum ellips adalah 2b²/a. Jika panjang setengah latus rektum dinotasikan dengan l maka

$l=\frac{b^{2}}{a}$

Sebuah ellips dapat dibuat sketsa grafiknya secara kasar dengan memperhatikan ujung-ujung sumbu mayor dan minor dan ujung latus rektum, dan dengan menggunakan kenyataan bahwa grafinya simetrik terhadap kedua sumbu.

Contoh soal
Diketahui persamaan elips $\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1$
Tentukan :

eksentrisitas
persamaan direktris
panjang latus rectum

Jawab :
dari persamaan diketahui
a² = 25 maka a = 5
b² = 9 maka b = 3
c² = a² – b² = 25 – 9 = 16 maka c = 4

Menentukan Eksentrisitas
e = c/a = 4/5 = 0,8

Menentukan persamaan direktris
Jarak pusat ke direktris = a/e = 5/0,8 = 6,25

Jadi persamaan direktrisnya x = –3,25 dan x = 9,25

Menentukan panjang latus rectum
Latus rectum merupakan tali busur elips yang melalui fokus dan tegak lurus sumbu utama. untuk menentukan panjang lactus rectum menggunakan rumus di atas

l = 2b²/a
= 2.3²/5
= 18/5
jadi panjang Latus Rectum adalah 18/5

Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran

Posted byNyach

Sesuai dengan kurikulum K13 Materi tentang Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaranadalah materi Mata Pelajaran Matematika Peminatan kelas XI Program IPA. Untuk memudahkan dalam mempelajari materi ini, sebaiknya kita baca dulu materi "persamaan lingkaran". Materi Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran kita bagi menjadi beberapa bagian yaitu kuasa suatu titik terhadap lingkaran; garis kuasa dan titik kuasa pada dua lingkaran ; dan garis kuasa dan titik kuasa pada tiga lingkaran.

Kuasa Suatu Titik terhadap Lingkaran
Misalkan ada titik T(

x_{1}, y_{1}

) diluar lingkaran, dan ada lingkaran L yang berpusat di titik P dan jari-jari

r

seperti gambar berikut.

Kuasa titik T(

x_{1}, y_{1}

) terhadap lingkaran L didefinisikan sebagai nilai

T P^{2} - r^{2}

♠

Menentukan nilai kuasa suatu titik yang dilambangkan K :
Misalkan ada persamaan lingkaran
L :

x^{2} + y^{2} + A x + B y + C = 0

dengan pusat

P (- \frac{A}{2}, - \frac{B}{2})

dan kuadrat jari-jarinya

r^{2} = \frac{1}{4} A^{2} + \frac{1}{4} B^{2} - C

.
Kuasa (K) titik T(

x_{1}, y_{1}

) terhadap lingkaran L, adalah

K = T P^{2} - r^{2} = {(x_{1} + \frac{1}{2} A)}^{2} + {(y_{1} + \frac{1}{2} B)}^{2} - r^{2}

atau

K = x_{1}^{2} + y_{1}^{2} + A x_{1} + B y_{1} + C

Perhatikan bahwa kuasa titik T(

x_{1}, y_{1}

) terhadap lingkaran

L : x^{2} + y^{2} + A x + B y + C = 0

dapat diperoleh dengan cara menggantikan

x

dan

y

pada persamaan lingkaran itu dengan

x_{1}

dan

y_{1}

♣

Kegunaan nilai kuasa suatu titik pada lingkaran
Setelah diperoleh kuasa suatu titik terhadap lingkaran, maka nilai kuasanya bisa digunakan untuk menentukan letak titik tersebut terhadap lingkaran, yaitu :
i). Jika

K > 0,

maka titik ada di luar lingkaran.
ii). Jika

K = 0,

maka titik terletak pada lingkaran.
iii). Jika

K < 0,

maka titik terletak di dalam lingkaran.

Contoh :
Tentukan kuasa titik T(1,2) terhadap lingkaran-lingkaran :
a).

x^{2} + y^{2} + 2 x - 4 y + 6 = 0

b).

(x - 2)^{2} + (y + 1)^{2} = 4

Penyelesaian :
*). Substitusi titik T(1,2) ke persamaan lingkaran
a). K =

1^{2} + 2^{2} + 2.1 - 4.2 + 6 = 5

b). Nol kan ruas kanan persamaan lingkaran.

(x - 2)^{2} + (y + 1)^{2} = 4 \to (x - 2)^{2} + (y + 1)^{2} - 4 = 0

K = (1 - 2)^{2} + (2 + 1)^{2} - 4 = 6

Karena nilai kuasa titik terhadap kedua lingkaran di atas positif (

K > 0

), maka titik T(1,2) terletak di luar kedua lingkaran.

Titik Kuasa dan Garis Kuasa Dua Lingkaran

Garis Kuasa
Misalkan ada dua buah lingkaran, dan terdapat titik yang memiliki kuasa yang sama terhadap kedua lingkaran tersebut. Himpunan semua titik kuasa (memiliki kuasa yang sama terhadap dua lingkaran) akan membentuk suatu garis yang dinamakan sebagai garis kuasa. Garis kuasa tegak lurus dengan garis yang menghubungkan dua pusat lingkaran.

Cara menentukan garis kuasa :
Misalkan ada dua lingkaran yaitu

L_{1} : x^{2} + y^{2} + A_{1} x + B_{1} y + C_{1} = 0

dan

L_{2} : x^{2} + y^{2} + A_{2} x + B_{2} y + C_{2} = 0

.
Garis kuasanya adalah :

L_{1} - L_{2} = 0

atau

(A_{1} - A_{2}) x + (B_{1} - B_{2}) y + (C_{1} - C_{2}) = 0

$♣$ Titik Kuasa
Titik Kuasa adalah titik yang terletak pada garis kuasa dan mempunyai kuasa yang sama terhadap kedua lingkaran.

Cara Menentukan titik kuasa :
Substitusi sebarang nilai salah satu variabelnya (misalkan pilih salah satu nilai

x_{1}

) ke persamaan garis kuasa, akan diperoleh nilai

y_{1}

. Titik (

x_{1}, y_{1}

) ini lah disebut sebagai salah satu titik kuasa kedua lingkaran.

Contoh :
Diketahui dua persamaan lingkaran :

L_{1} : x^{2} + y^{2} + 2 x - 2 y - 6 = 0

dan

L_{2} : x^{2} + y^{2} - 12 x - 4 y + 36 = 0

a). Tentukan persamaan garis kuasanya;
b). Tentukan titik kuasanya pada sumbu X dan kuasanya pada kedua lingkaran.
c). Tentukan titik kuasanya pada sumbu Y dan kuasanya pada kedua lingkaran.
Penyelesaian :
a). Menentukan garis kuasa :

L_{1} - L_{2} = 0

\begin{array}{cc} x^{2} + y^{2} + 2 x - 2 y - 6 = 0 \\ x^{2} + y^{2} - 12 x - 4 y + 36 = 0 & - \\ 14 x + 2 y - 42 = 0 \\ 7 x + y = 21 \end{array}

garis kuasanya adalah

7 x + y = 21

b). Titik kuasa pada sumbu X, artinya kita mencari titik pada garis kuasa yang memotong sumbu X, caranya adalah substitusi

y = 0

ke garis kuasa, diperoleh :

y = 0 \to 7 x + y = 21 \to 7 x + 0 = 21 \to x = 3

artinya titik kuasa pada sumbu X adalah titik (3,0).
*). Kuasa titik (3,0) terhadap lingkaran :
Substitusi titik (3,0) ke salah satu lingkaran saja (karena kuasanya sama) ,

L_{1} : x^{2} + y^{2} + 2 x - 2 y - 6 = 0 \to K = 3^{2} + 0^{2} + 2.3 - 2.0 - 6 = 9

kuasa titik (3,0) adalah 9.

c). Titik kuasa pada sumbu Y, artinya kita mencari titik pada garis kuasa yang memotong sumbu Y, caranya adalah substitusi

x = 0

ke garis kuasa, diperoleh :

x = 0 \to 7 x + y = 21 \to 7.0 + y = 21 \to= 21

artinya titik kuasa pada sumbu Y adalah titik (0,21).
*). Kuasa titik (0,21) terhadap lingkaran :
Substitusi titik (0,21) ke salah satu lingkaran saja (karena kuasanya sama) ,

L_{1} : x^{2} + y^{2} + 2 x - 2 y - 6 = 0 \to K = 0^{2} + 21^{2} + 2.0 - 2.21 - 6 = 393

kuasa titik (0,21) adalah 393.
Berikut gambar lingkaran dan garis kuasanya :

Semoga sukses, demikian materi tentang Titik kuasa dan garis kuasa irisan dua lingkaran.

Info Math SMA

Polinomial (suku banyak) dan Metode Horner

Polinomial (suku banyak) dan Metode Horner

Pembagian suku banyak yang tidak linier

Soal dan Pembahasa Aplikasi Turunan Fungsi

Soal Turunan Fungsi Aljabar dan Pembahasannya (Latihan siswa kelas XI program IPS) KTSP

Soal Fungsi komposisi (kelas XI IPS) KTSP

Menentukan peluang Kejadian Binomial

Panjang Latus Rectum Pada Elips

Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran

SOAL TES ONLINE

Followers

Subscribe via email

Entri Populer

Menu

Indicator Visitor Info Math

Pageviews past week

Blog Archive