Menentukan peluang Kejadian Binomial
Menentukan peluang Kejadian Binomial - Distribusi Binomial adalah salah satu materi kelas XI pada kurikulum 2013.Dalam teori probabilitas dan statistika, Distribusi Binomial
adalah distribusi probabilitas diskret jumlah keberhasilan dalam n
percobaan ya/tidak yang saling bebas, dimana setiap hasil percobaan
memiliki
probabilitas p.Pengertian tersebut menurut wikipedia.org
Ciri-ciri percobaan binomial yaitu sebagai berikut.
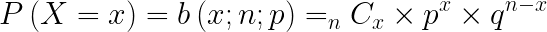
dengan x = 0, 1, 2, 3, ..., n
Keterangan :
n : banyak percobaan
x : banyak berhasil
p : peluang berhasil
q : peluang gagal (q = 1-p)
Contoh Soal Dan Pembahasan
n = 8
x = 5
p = 1/2
q = 1-p = 1- 1/2 = 1/2
Ditanya : peluang muncul gambar sebanyak 5 kali
Jawab :
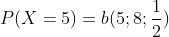
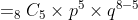
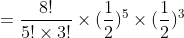
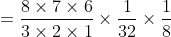
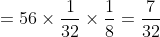
Jadi, peluang muncul gambar sebanyak 5 kali adalah 7/32
n = 5
x = 2
p = 1/6
q = 1-1/6 = 5/6
Ditanya : peluang muncul mata dadu 4 sebanyak 2 kali
Jawab :

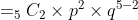
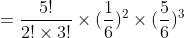
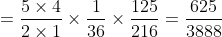
Jadi, peluang muncul mata dadu 4 sebanyak 2 kali adalah 625/3888 UNIQUE TRADISIONAL @ INDONESIA, U KNOW ?? KLIK HERE PLEASE
probabilitas p.Pengertian tersebut menurut wikipedia.org
Ciri-ciri percobaan binomial yaitu sebagai berikut.
- Setiap percobaan dibedakan menjadi 2 jenis kejadian yang keduanya saling lepas
- Hasil dari percobaan tersebut hanya 2 macam, yaitu berhasil dan gagal
- Peluang kejadian berhasil adalah p dan peluang kejadian gagal adalah q = 1-p
- Masing-masing percobaan bersifat saling bebas, artinya hasil percobaan pertama tidak memengaruhi hasil percobaan berikutnya.
dengan x = 0, 1, 2, 3, ..., n
Keterangan :
n : banyak percobaan
x : banyak berhasil
p : peluang berhasil
q : peluang gagal (q = 1-p)
Contoh Soal Dan Pembahasan
- Sebuah mata uang logam dilemparkan sebanyak 8 kali.Berapa peluang muncul gambar sebanyak 5 kali?
n = 8
x = 5
p = 1/2
q = 1-p = 1- 1/2 = 1/2
Ditanya : peluang muncul gambar sebanyak 5 kali
Jawab :
Jadi, peluang muncul gambar sebanyak 5 kali adalah 7/32
- Sebuah dadu dilemparkan sebanyak 5 kali.Berapa peluang muncul mata dadu 4 sebanyak 2 kali?
n = 5
x = 2
p = 1/6
q = 1-1/6 = 5/6
Ditanya : peluang muncul mata dadu 4 sebanyak 2 kali
Jawab :
Jadi, peluang muncul mata dadu 4 sebanyak 2 kali adalah 625/3888 UNIQUE TRADISIONAL @ INDONESIA, U KNOW ?? KLIK HERE PLEASE
0 komentar:
Post a Comment