Info Math SMA

Sesuai dengan kurikulum K13 Materi tentang Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaranadalah materi Mata Pelajaran Matematika Peminatan kelas XI Program IPA. Untuk memudahkan dalam mempelajari materi ini, sebaiknya kita baca dulu materi "persamaan lingkaran". Materi Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran kita bagi menjadi beberapa bagian yaitu kuasa suatu titik terhadap lingkaran; garis kuasa dan titik kuasa pada dua lingkaran ; dan garis kuasa dan titik kuasa pada tiga lingkaran.

Kuasa Suatu Titik terhadap Lingkaran
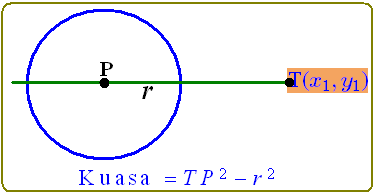
Misalkan ada titik T(x1,y1) diluar lingkaran, dan ada lingkaran L yang berpusat di titik P dan jari-jari r seperti gambar berikut.

Kuasa titik T(x1,y1) terhadap lingkaran L didefinisikan sebagai nilai TP2−r2 .

♠ Menentukan nilai kuasa suatu titik yang dilambangkan K :
       Misalkan ada persamaan lingkaran
L : x2+y2+Ax+By+C=0 dengan pusat P(−A2,−B2) dan kuadrat jari-jarinya r2=14A2+14B2−C .
Kuasa (K) titik T(x1,y1) terhadap lingkaran L, adalah
K=TP2−r2=(x1+12A)2+(y1+12B)2−r2 atau
K=x21+y21+Ax1+By1+C
       Perhatikan bahwa kuasa titik T(x1,y1) terhadap lingkaran L:x2+y2+Ax+By+C=0 dapat diperoleh dengan cara menggantikan x dan y pada persamaan lingkaran itu dengan x1 dan y1 .

♣ Kegunaan nilai kuasa suatu titik pada lingkaran
Setelah diperoleh kuasa suatu titik terhadap lingkaran, maka nilai kuasanya bisa digunakan untuk menentukan letak titik tersebut terhadap lingkaran, yaitu :
i). Jika K>0, maka titik ada di luar lingkaran.
ii). Jika K=0, maka titik terletak pada lingkaran.
iii). Jika K<0, maka titik terletak di dalam lingkaran.

Contoh :
Tentukan kuasa titik T(1,2) terhadap lingkaran-lingkaran :
a). x2+y2+2x−4y+6=0
b). (x−2)2+(y+1)2=4
Penyelesaian :
*). Substitusi titik T(1,2) ke persamaan lingkaran
a). K = 12+22+2.1−4.2+6=5
b). Nol kan ruas kanan persamaan lingkaran.
(x−2)2+(y+1)2=4→(x−2)2+(y+1)2−4=0
K=(1−2)2+(2+1)2−4=6
Karena nilai kuasa titik terhadap kedua lingkaran di atas positif (K>0), maka titik T(1,2) terletak di luar kedua lingkaran. 

Titik Kuasa dan Garis Kuasa Dua Lingkaran

Garis Kuasa
       Misalkan ada dua buah lingkaran, dan terdapat titik yang memiliki kuasa yang sama terhadap kedua lingkaran tersebut. Himpunan semua titik kuasa (memiliki kuasa yang sama terhadap dua lingkaran) akan membentuk suatu garis yang dinamakan sebagai garis kuasa. Garis kuasa tegak lurus dengan garis yang menghubungkan dua pusat lingkaran.




 Cara menentukan garis kuasa :
Misalkan ada dua lingkaran yaitu
L1:x2+y2+A1x+B1y+C1=0 dan
L2:x2+y2+A2x+B2y+C2=0 .
Garis kuasanya adalah :
L1−L2=0 atau (A1−A2)x+(B1−B2)y+(C1−C2)=0

Titik Kuasa
       Titik Kuasa adalah titik yang terletak pada garis kuasa dan mempunyai kuasa yang sama terhadap kedua lingkaran.

Cara Menentukan titik kuasa :
Substitusi sebarang nilai salah satu variabelnya (misalkan pilih salah satu nilai x1 ) ke persamaan garis kuasa, akan diperoleh nilai y1 . Titik (x1,y1) ini lah disebut sebagai salah satu titik kuasa kedua lingkaran.


Contoh :
Diketahui dua persamaan lingkaran :
L1:x2+y2+2x−2y−6=0 dan L2:x2+y2−12x−4y+36=0
a). Tentukan persamaan garis kuasanya;
b). Tentukan titik kuasanya pada sumbu X dan kuasanya pada kedua lingkaran.
c). Tentukan titik kuasanya pada sumbu Y dan kuasanya pada kedua lingkaran.
Penyelesaian :
a). Menentukan garis kuasa : L1−L2=0
x2+y2+2x−2y−6=0x2+y2−12x−4y+36=014x+2y−42=07x+y=21−
garis kuasanya adalah 7x+y=21

b). Titik kuasa pada sumbu X, artinya kita mencari titik pada garis kuasa yang memotong sumbu X, caranya adalah substitusi y=0 ke garis kuasa, diperoleh :
y=0→7x+y=21→7x+0=21→x=3
artinya titik kuasa pada sumbu X adalah titik (3,0).
*). Kuasa titik (3,0) terhadap lingkaran :
Substitusi titik (3,0) ke salah satu lingkaran saja (karena kuasanya sama) ,
L1:x2+y2+2x−2y−6=0→K=32+02+2.3−2.0−6=9
kuasa titik (3,0) adalah 9.

c). Titik kuasa pada sumbu Y, artinya kita mencari titik pada garis kuasa yang memotong sumbu Y, caranya adalah substitusi x=0 ke garis kuasa, diperoleh :
x=0→7x+y=21→7.0+y=21→=21
artinya titik kuasa pada sumbu Y adalah titik (0,21).
*). Kuasa titik (0,21) terhadap lingkaran :
Substitusi titik (0,21) ke salah satu lingkaran saja (karena kuasanya sama) ,
L1:x2+y2+2x−2y−6=0→K=02+212+2.0−2.21−6=393
kuasa titik (0,21) adalah 393.
Berikut gambar lingkaran dan garis kuasanya :
 Semoga sukses,  demikian materi tentang Titik kuasa dan garis kuasa irisan dua lingkaran.




UNIQUE TRADISIONAL @ INDONESIA, U KNOW ?? KLIK HERE PLEASE