Info Math SMA

Tentang panjang latus rectum pada Elips ini materi yang terasa kurang viral (terkenal) atau boming. Latus Rectum paling terkenal saat pembahasan Irisan kerucut tentang Parabola. Definisi Latus Rectum pada elips adalah tali busur yang melalui salah satu fokus dan tegak lurus dengan sumbu mayor.

Sedangkan titik potong latus rektum dengan ellips disebut latera rekta. Untuk mencari panjang latus rektum diberikan nilai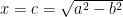 pada persamaan (4) dan dengan menyelesaikan persamaan untuk y diperoleh y = b²/a. Jadi latera rekta ellips (4) adalah L(c, b²/a) dan R(c, –b²/a), sehingga panjang latus rektum ellips adalah 2b²/a. Jika panjang setengah latus rektum dinotasikan dengan l maka
Sebuah ellips dapat dibuat sketsa grafiknya secara kasar dengan memperhatikan ujung-ujung sumbu mayor dan minor dan ujung latus rektum, dan dengan menggunakan kenyataan bahwa grafinya simetrik terhadap kedua sumbu.

Contoh soal
Diketahui persamaan elips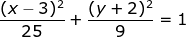 
Tentukan :

• eksentrisitas
• persamaan direktris
• panjang latus rectum

Jawab :
dari persamaan diketahui
a² = 25 maka a = 5
b² = 9 maka b = 3
c² = a² – b² = 25 – 9 = 16 maka c = 4

Menentukan Eksentrisitas
e = c/a = 4/5 = 0,8

Menentukan persamaan direktris
Jarak pusat ke direktris = a/e = 5/0,8 = 6,25


Jadi persamaan direktrisnya x = –3,25 dan x = 9,25

 Menentukan panjang latus rectum
Latus rectum merupakan tali busur elips yang melalui fokus dan tegak lurus sumbu utama. untuk menentukan panjang lactus rectum menggunakan rumus di atas

 l = 2b²/a
   = 2.3²/5
   = 18/5
jadi panjang Latus Rectum adalah 18/5
UNIQUE TRADISIONAL @ INDONESIA, U KNOW ?? KLIK HERE PLEASE

Sesuai dengan kurikulum K13 Materi tentang Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaranadalah materi Mata Pelajaran Matematika Peminatan kelas XI Program IPA. Untuk memudahkan dalam mempelajari materi ini, sebaiknya kita baca dulu materi "persamaan lingkaran". Materi Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran kita bagi menjadi beberapa bagian yaitu kuasa suatu titik terhadap lingkaran; garis kuasa dan titik kuasa pada dua lingkaran ; dan garis kuasa dan titik kuasa pada tiga lingkaran.

Kuasa Suatu Titik terhadap Lingkaran
Misalkan ada titik T(x1,y1) diluar lingkaran, dan ada lingkaran L yang berpusat di titik P dan jari-jari r seperti gambar berikut.

Kuasa titik T(x1,y1) terhadap lingkaran L didefinisikan sebagai nilai TP2−r2 .

♠ Menentukan nilai kuasa suatu titik yang dilambangkan K :
       Misalkan ada persamaan lingkaran
L : x2+y2+Ax+By+C=0 dengan pusat P(−A2,−B2) dan kuadrat jari-jarinya r2=14A2+14B2−C .
Kuasa (K) titik T(x1,y1) terhadap lingkaran L, adalah
K=TP2−r2=(x1+12A)2+(y1+12B)2−r2 atau
K=x21+y21+Ax1+By1+C
       Perhatikan bahwa kuasa titik T(x1,y1) terhadap lingkaran L:x2+y2+Ax+By+C=0 dapat diperoleh dengan cara menggantikan x dan y pada persamaan lingkaran itu dengan x1 dan y1 .

♣ Kegunaan nilai kuasa suatu titik pada lingkaran
Setelah diperoleh kuasa suatu titik terhadap lingkaran, maka nilai kuasanya bisa digunakan untuk menentukan letak titik tersebut terhadap lingkaran, yaitu :
i). Jika K>0, maka titik ada di luar lingkaran.
ii). Jika K=0, maka titik terletak pada lingkaran.
iii). Jika K<0, maka titik terletak di dalam lingkaran.

Contoh :
Tentukan kuasa titik T(1,2) terhadap lingkaran-lingkaran :
a). x2+y2+2x−4y+6=0
b). (x−2)2+(y+1)2=4
Penyelesaian :
*). Substitusi titik T(1,2) ke persamaan lingkaran
a). K = 12+22+2.1−4.2+6=5
b). Nol kan ruas kanan persamaan lingkaran.
(x−2)2+(y+1)2=4→(x−2)2+(y+1)2−4=0
K=(1−2)2+(2+1)2−4=6
Karena nilai kuasa titik terhadap kedua lingkaran di atas positif (K>0), maka titik T(1,2) terletak di luar kedua lingkaran. 

Titik Kuasa dan Garis Kuasa Dua Lingkaran

Garis Kuasa
       Misalkan ada dua buah lingkaran, dan terdapat titik yang memiliki kuasa yang sama terhadap kedua lingkaran tersebut. Himpunan semua titik kuasa (memiliki kuasa yang sama terhadap dua lingkaran) akan membentuk suatu garis yang dinamakan sebagai garis kuasa. Garis kuasa tegak lurus dengan garis yang menghubungkan dua pusat lingkaran.




 Cara menentukan garis kuasa :
Misalkan ada dua lingkaran yaitu
L1:x2+y2+A1x+B1y+C1=0 dan
L2:x2+y2+A2x+B2y+C2=0 .
Garis kuasanya adalah :
L1−L2=0 atau (A1−A2)x+(B1−B2)y+(C1−C2)=0

Titik Kuasa
       Titik Kuasa adalah titik yang terletak pada garis kuasa dan mempunyai kuasa yang sama terhadap kedua lingkaran.

Cara Menentukan titik kuasa :
Substitusi sebarang nilai salah satu variabelnya (misalkan pilih salah satu nilai x1 ) ke persamaan garis kuasa, akan diperoleh nilai y1 . Titik (x1,y1) ini lah disebut sebagai salah satu titik kuasa kedua lingkaran.


Contoh :
Diketahui dua persamaan lingkaran :
L1:x2+y2+2x−2y−6=0 dan L2:x2+y2−12x−4y+36=0
a). Tentukan persamaan garis kuasanya;
b). Tentukan titik kuasanya pada sumbu X dan kuasanya pada kedua lingkaran.
c). Tentukan titik kuasanya pada sumbu Y dan kuasanya pada kedua lingkaran.
Penyelesaian :
a). Menentukan garis kuasa : L1−L2=0
x2+y2+2x−2y−6=0x2+y2−12x−4y+36=014x+2y−42=07x+y=21−
garis kuasanya adalah 7x+y=21

b). Titik kuasa pada sumbu X, artinya kita mencari titik pada garis kuasa yang memotong sumbu X, caranya adalah substitusi y=0 ke garis kuasa, diperoleh :
y=0→7x+y=21→7x+0=21→x=3
artinya titik kuasa pada sumbu X adalah titik (3,0).
*). Kuasa titik (3,0) terhadap lingkaran :
Substitusi titik (3,0) ke salah satu lingkaran saja (karena kuasanya sama) ,
L1:x2+y2+2x−2y−6=0→K=32+02+2.3−2.0−6=9
kuasa titik (3,0) adalah 9.

c). Titik kuasa pada sumbu Y, artinya kita mencari titik pada garis kuasa yang memotong sumbu Y, caranya adalah substitusi x=0 ke garis kuasa, diperoleh :
x=0→7x+y=21→7.0+y=21→=21
artinya titik kuasa pada sumbu Y adalah titik (0,21).
*). Kuasa titik (0,21) terhadap lingkaran :
Substitusi titik (0,21) ke salah satu lingkaran saja (karena kuasanya sama) ,
L1:x2+y2+2x−2y−6=0→K=02+212+2.0−2.21−6=393
kuasa titik (0,21) adalah 393.
Berikut gambar lingkaran dan garis kuasanya :
 Semoga sukses,  demikian materi tentang Titik kuasa dan garis kuasa irisan dua lingkaran.




UNIQUE TRADISIONAL @ INDONESIA, U KNOW ?? KLIK HERE PLEASE